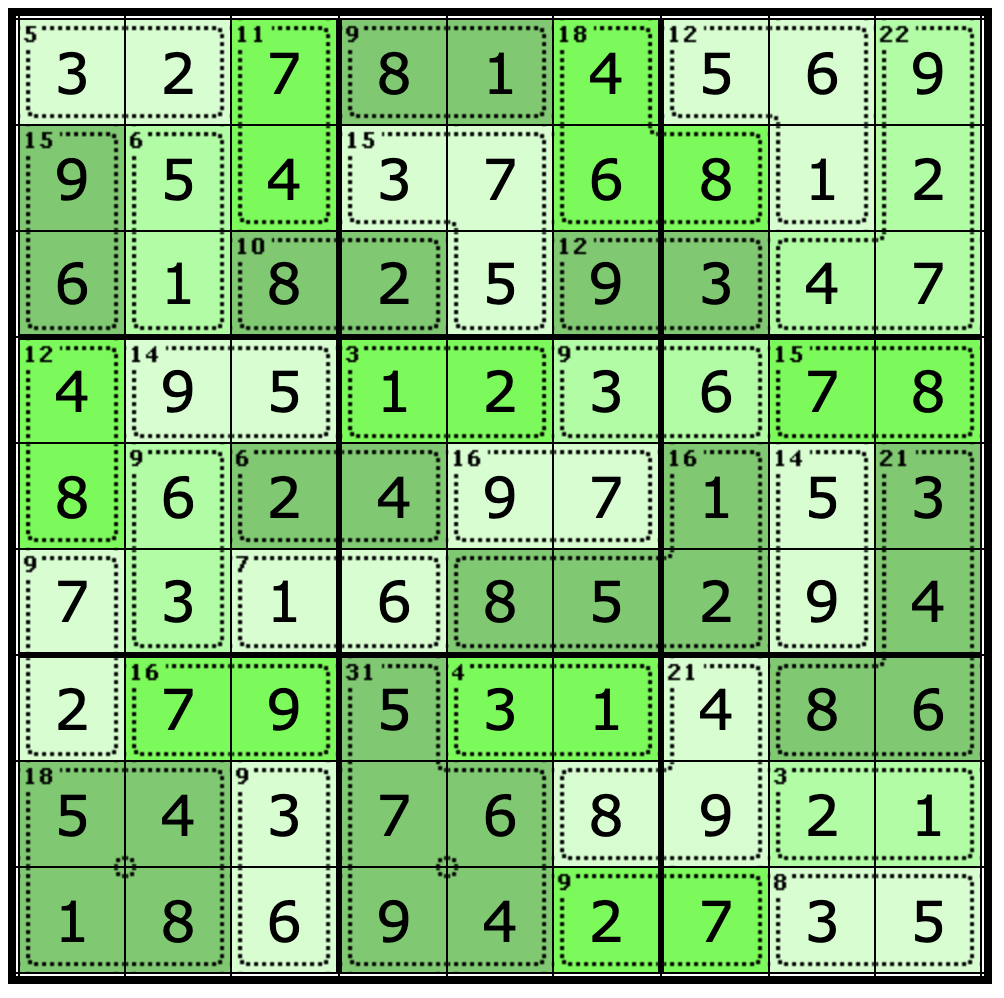
Killer Sudoku is an extremely addictive logic puzzle. Combining elements of Sudoku and Kakuro, it is a written number game that is played on a 9 x 9 grid, with the simple objective of filling all of the puzzle’s cells with the numbers 1 to 9. 

To solve a Killer Sudoku puzzle, players must use clue numbers and a set of basic rules which are similar to standard Sudoku rules. It is a high-entertaining, fun, and interesting game that will give you many hours of enjoyment.

Despite the name, many Killer Sudoku puzzles are easier than standard Sudoku puzzles, particularly if you have good mental arithmetic skills. However, the most difficult Killer Sudoku puzzles can take many hours to solve. 

In this comprehensive guide you will learn how to play the popular game of Killer Sudoku.

Let’s start by taking a look at a Killer Sudoku puzzle and identifying its different components. Check out the puzzle below.

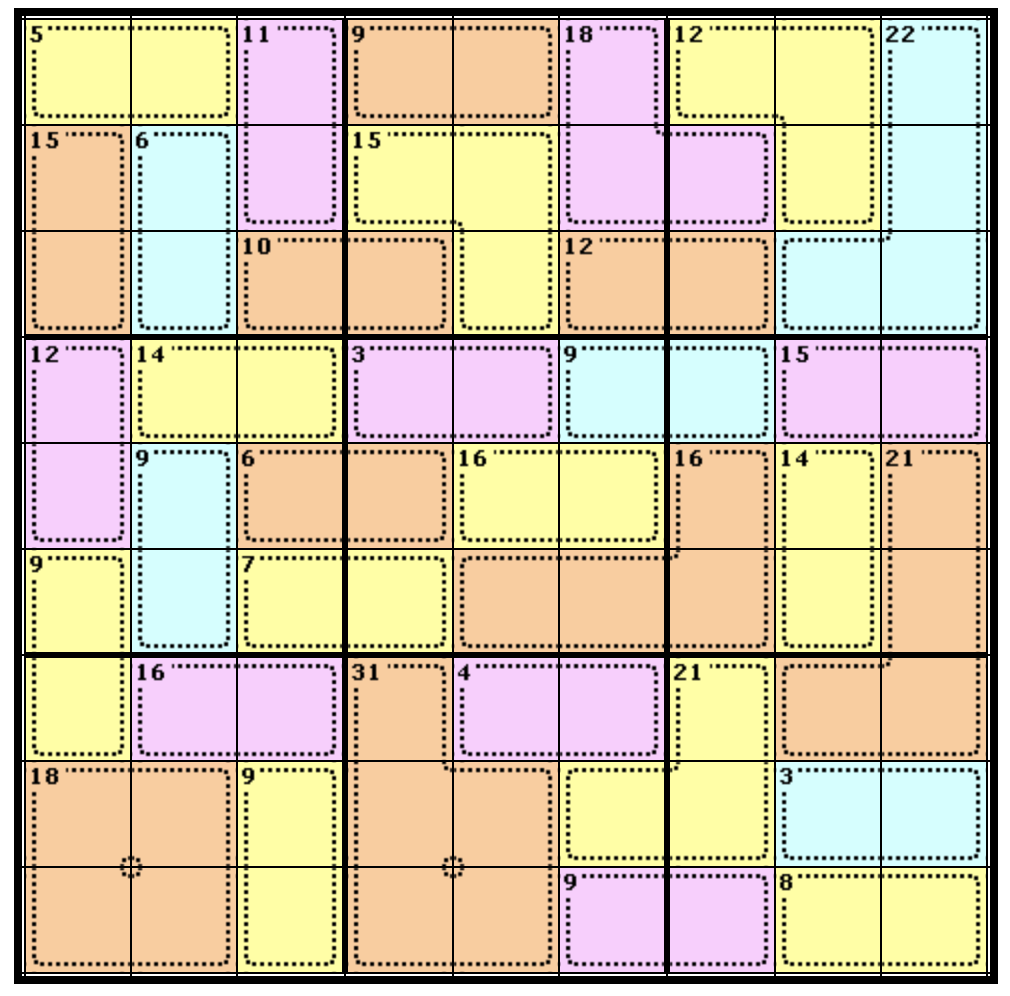
The names of the main components of the puzzle are:

Cell

A cell is one of small squares inside of the puzzle, into which you place a single number

Row

A row is a horizontal line of 9 cells. The numbers 1 to 9 can only appear once per row.

Column

A column is a vertical line of 9 cells. The numbers 1 to 9 can only appear once per column.

Nonet

This is a 3 x 3 grid of cells that sits within the puzzle. There are 9 of them in each puzzle, outlined by a thicker line (shown below).

Cage

The Cage is the colored sections of the puzzle. Each Cage will have a number in it, which represents the total value of the numbers in the Cage’s Squares. 

If we look at the top left corner of the puzzle above, you will see a yellow Cage cover 2 cells has the number 5 in it. This tells us that the total value of the numbers in those two squares adds up to 5. So, the values in the cells could be a 1 and 4 or a  2 and 3.

Cages are a unique feature of Killer Sudoku puzzles and do not appear in Sudoku or Kakuro puzzles.

House/Region

A house is any non-repeating set of 9 cells. This is sometimes used as a quick way of identifying a Column, Row, or Nonet. This is also referred to as a region.

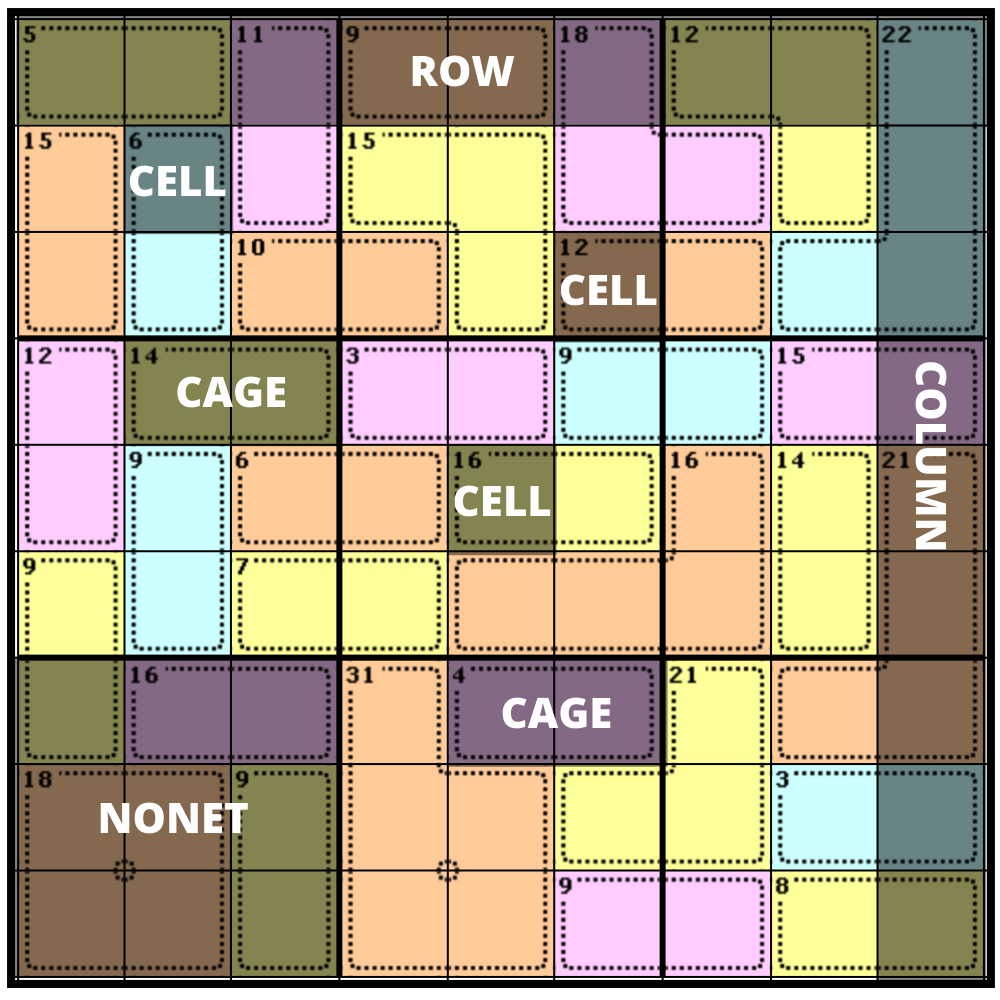
The image below has examples of  these components marked out.

As mentioned earlier, the goal of Killer Sudoku is to fill the cells with the numbers 1 to 9. However, the following restrictions apply:

    1. Only 1 number can be placed in each cell

You can’t attempt to squeeze a 1 and 2 into a single cell to complete the puzzle.

    2. Each row, column, and nonet can only contain unique numbers. 

You couldn’t have two 4’s appearing in the same row, column, or nonet. This is the standard rule for Sudoku.

    3. The sum of the numbers inside of a cage must equal the clue number

A Cage with two Cells and a clue of 3 must contain the numbers 2 and 1. Kakuro operates in a similar way. 

Solving the Puzzle

Let’s take another look at our puzzle and see if we can begin solving it.

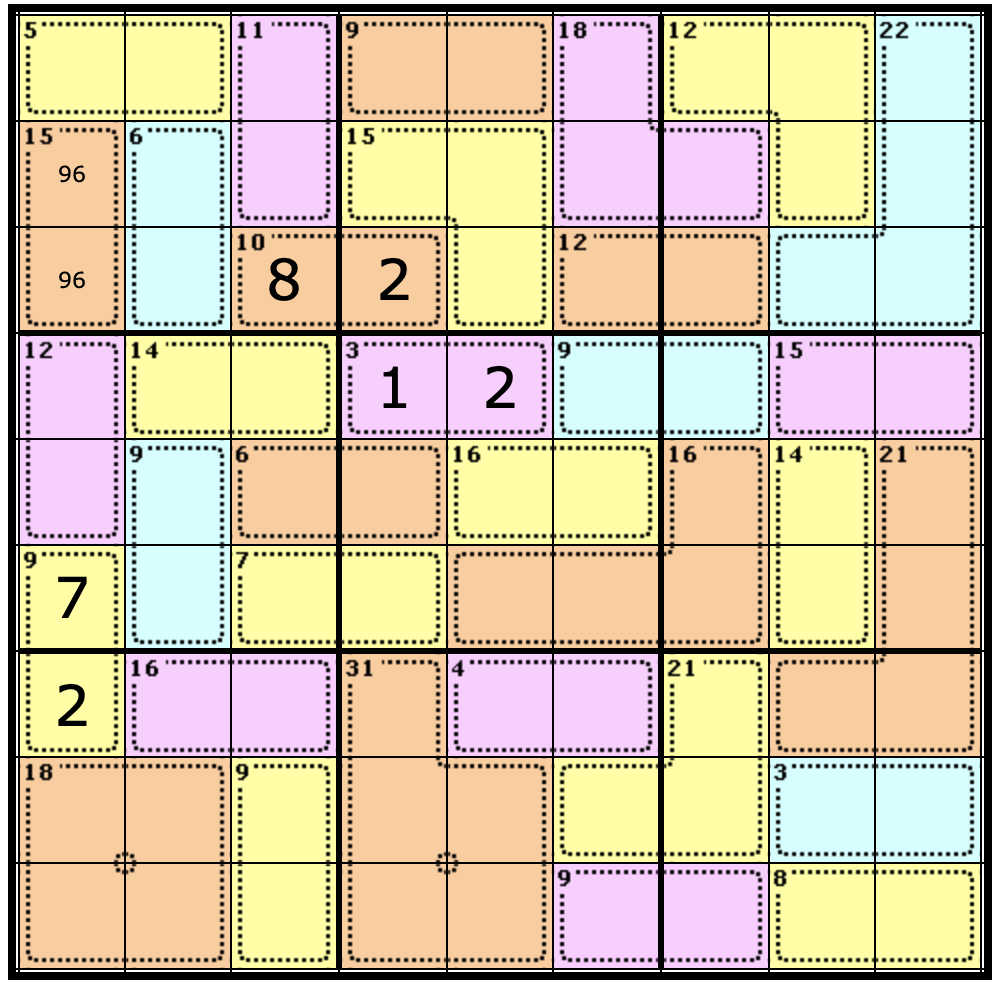
One of the greatest challenges faced by first-time players is deciding where to start. An easy way to find a starting point is by looking for a Region that contains multiple Cages and a single spare Cell. That’s because we can apply the Rule of 45 to discover what that spare cell contains. It is a very handy rule that will help you solve many puzzles. For example, look at the Nonet on the lower left of the puzzle (marked in black).

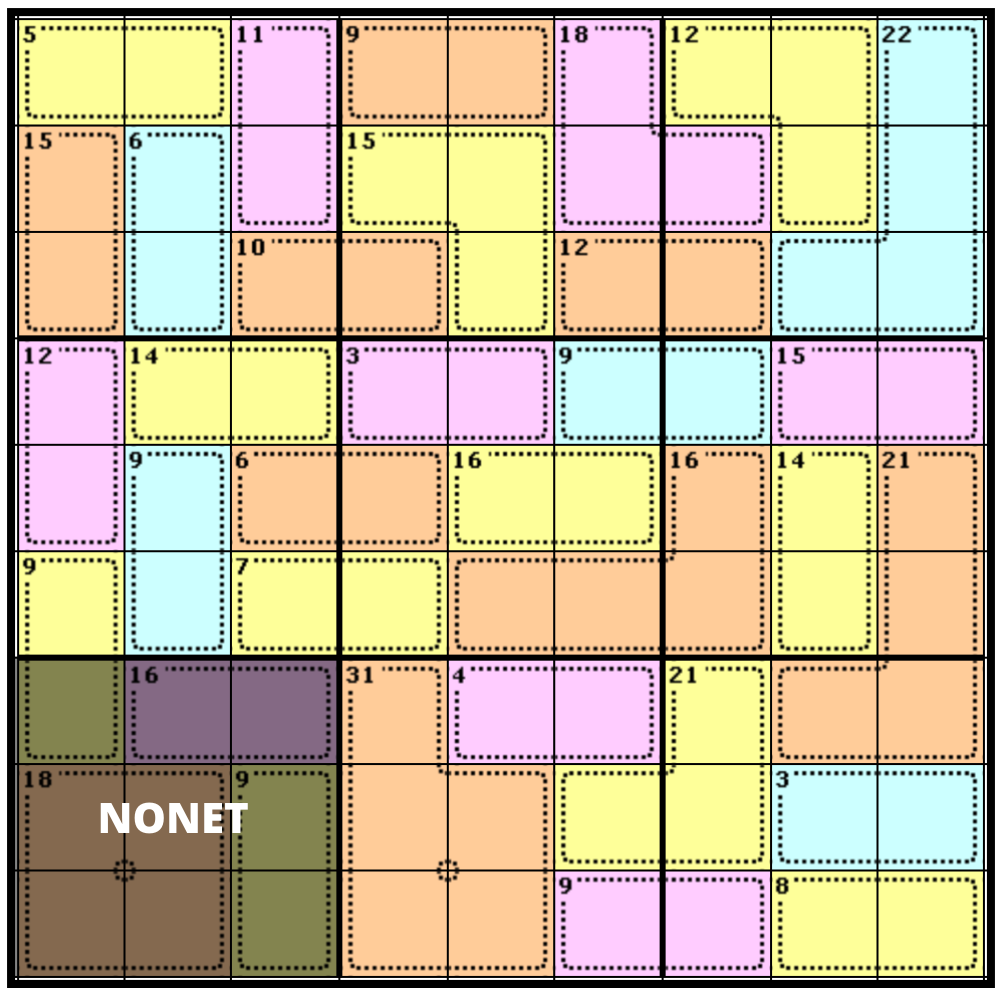
Notice that it holds 3 complete Cages, which have clues of 16, 18, and 9. It also holds a single cell which is half of a Cage of 9. What is the significance of this? It means we can apply the rule of 45 to determine the value of the standalone Cell.

The rule of 45 states that the Cells in each Row, Cell, or Nonet must add up to 45. That’s because the sum of 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45.

So, if we look at the Nonet on the lower left, we know that the value of the Cells in the complete Cages will equal 18 + 16 + 9 (43 in total).

That means the remaining square must equal 2, because all completed regions must add up to 45. Let’s add our 2: 

Pretty clever right? This simple technique is used a lot when solving Killer Sudoku puzzles. Now, look at the Cage where we just added our 2. That Cage’s clue is 9, which means the other Cell must be a 7. We know this because of the Rule of Necessity (the two squares must add up to 9 to match the clue).

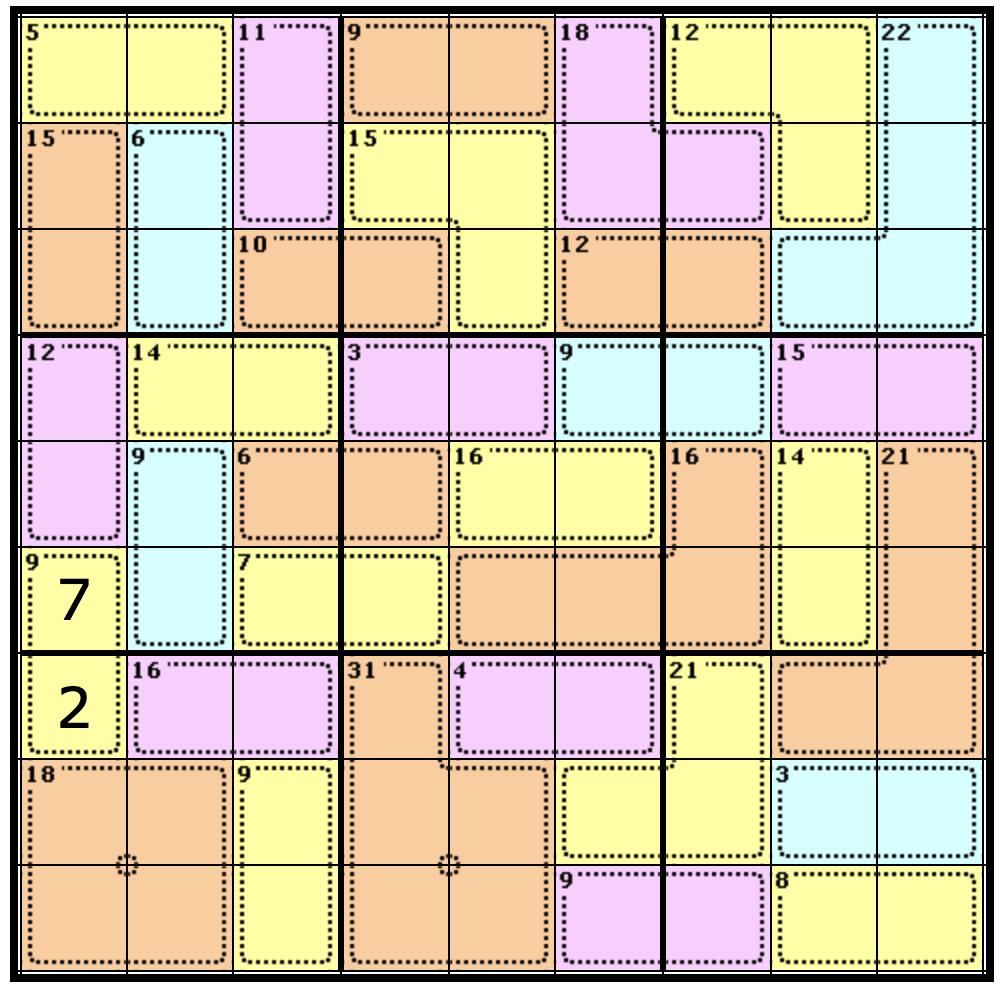
Congratulations, you just used the Rule of 45 and the Rule of Necessity to complete a Cage! We’ll review these rules again shortly. 

Can you see any other Segments which we can easily use the Rule of 45 on? Remember that this rule works on rows, columns, and nonets.

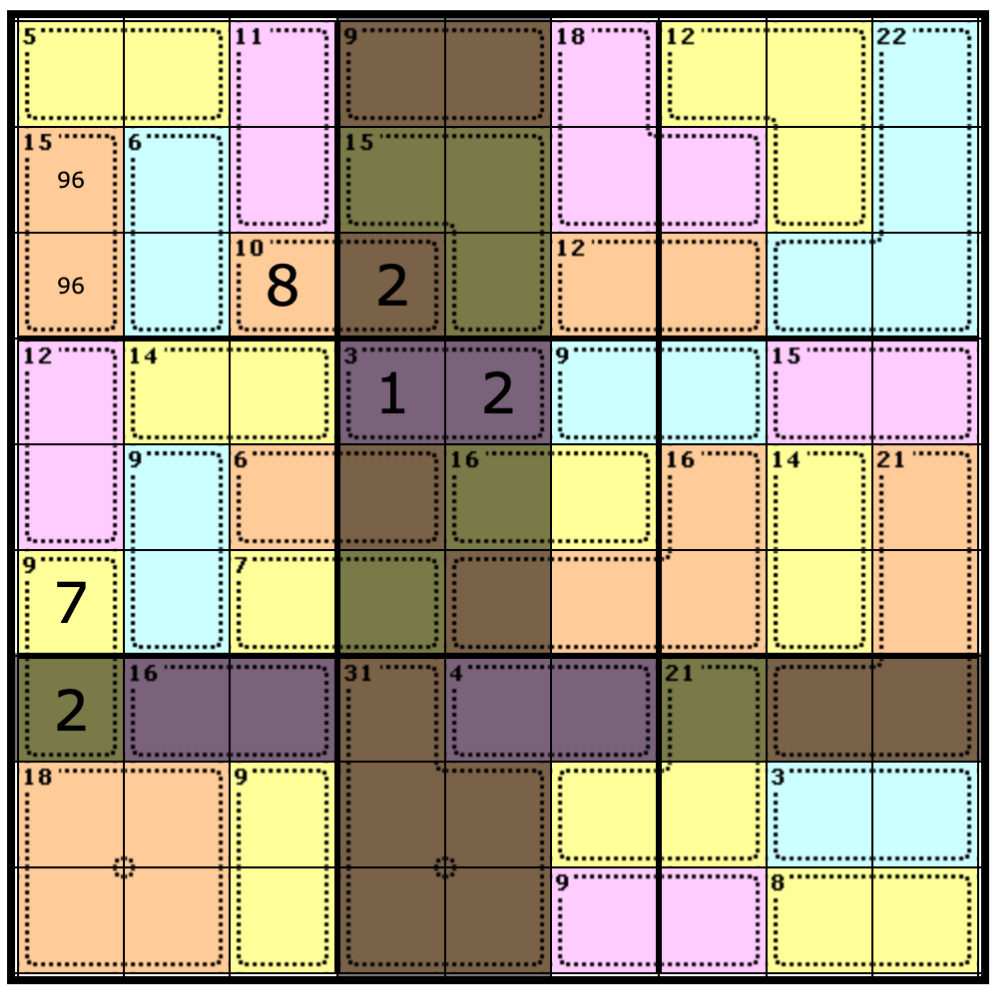
One that stands out to me is the Nonet on the top left. Take a second to see if you can calculate the value that goes in the Cage with the clue of 10.

If you answered 8, you would be correct. That’s because 45 - (5 + 11 + 6 + 15) = 8. Let’s fill that in.

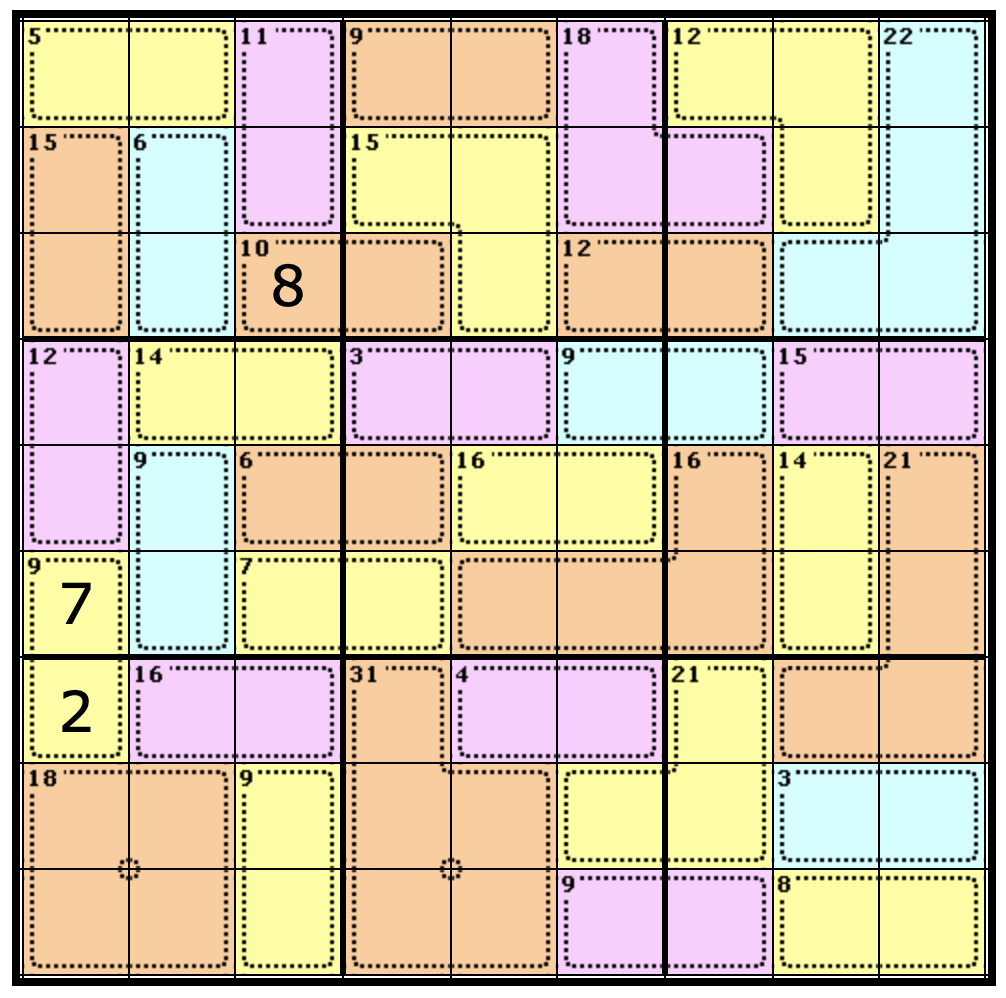
Again, you can use the rule of necessity to solve the rest of the Cage where we just placed out 8, like so:

Another great place to look for solving opportunities is Cages with low numbers. That’s because these Cages have very few available solving options. For example:

    • 3 cages can only contain 1 and 2

    • 4 cages can only contain 1 and 3

    • 5 cages can only contain 1 and 4 or 2 and 3

    • 6 cages with 2 squares can only contain 1 and 5 or 2 and 4

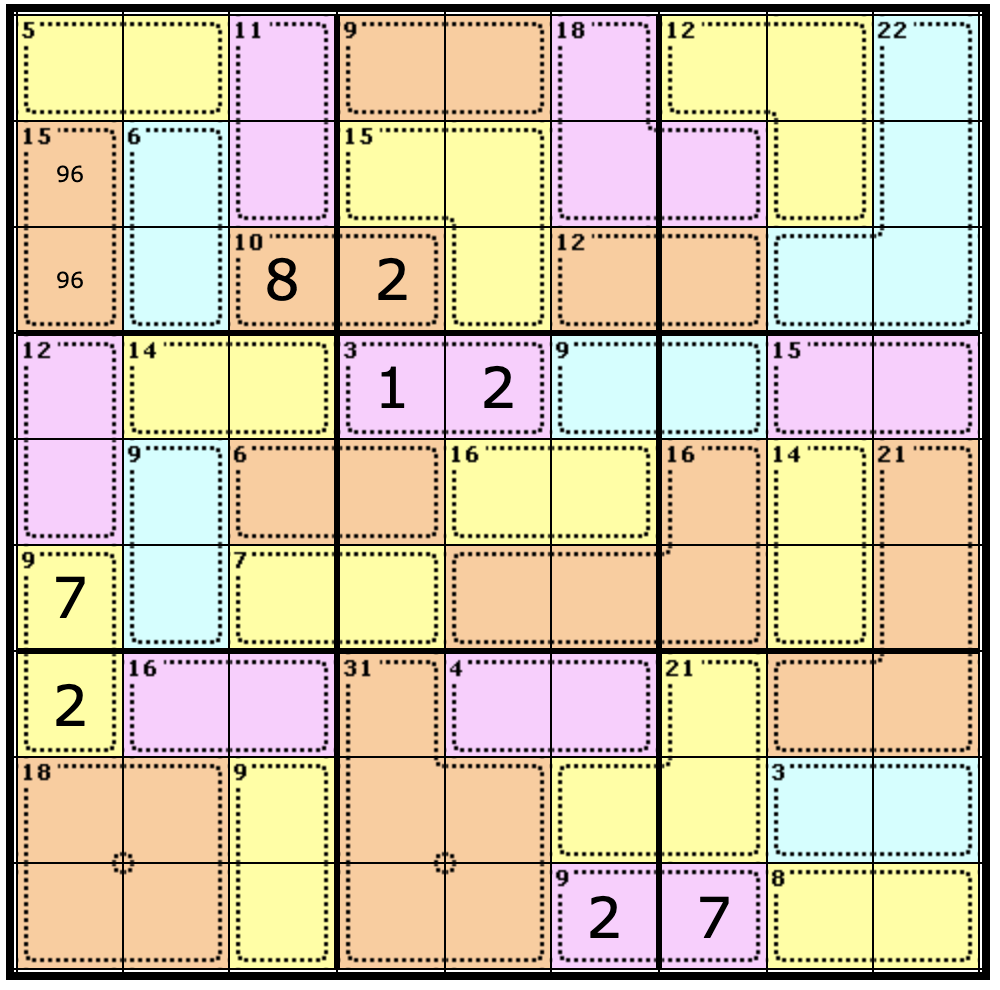
Now, take a look at the Cage below where we just entered our 2:

We know that 3 Cages can only contain the number 1 and 2. But which Cell holds the 1 and which one holds the 2? 

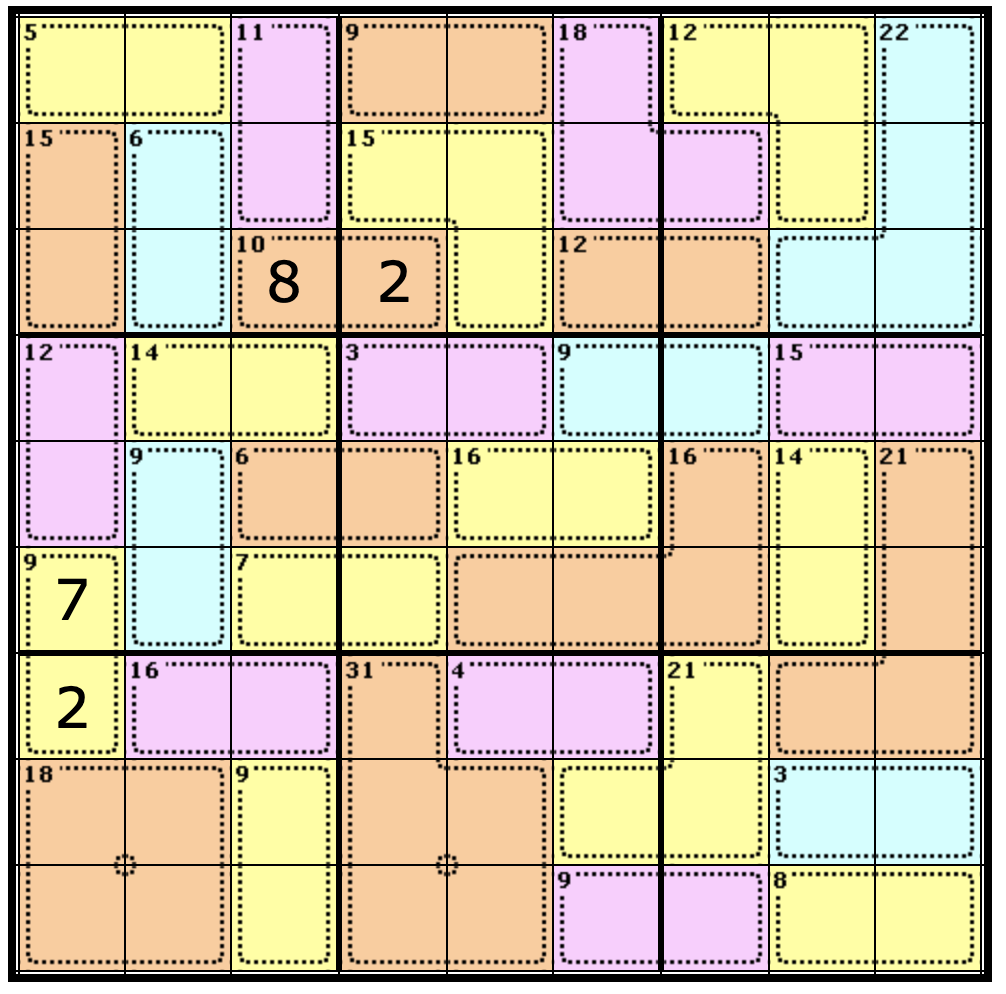
Well, remember the golden rule of Killer Sudoku, which states that each number can only appear once per column, row, or nonet. That means the Cell below the 2 must have a 1 and the other Cell must be a 2, like so:

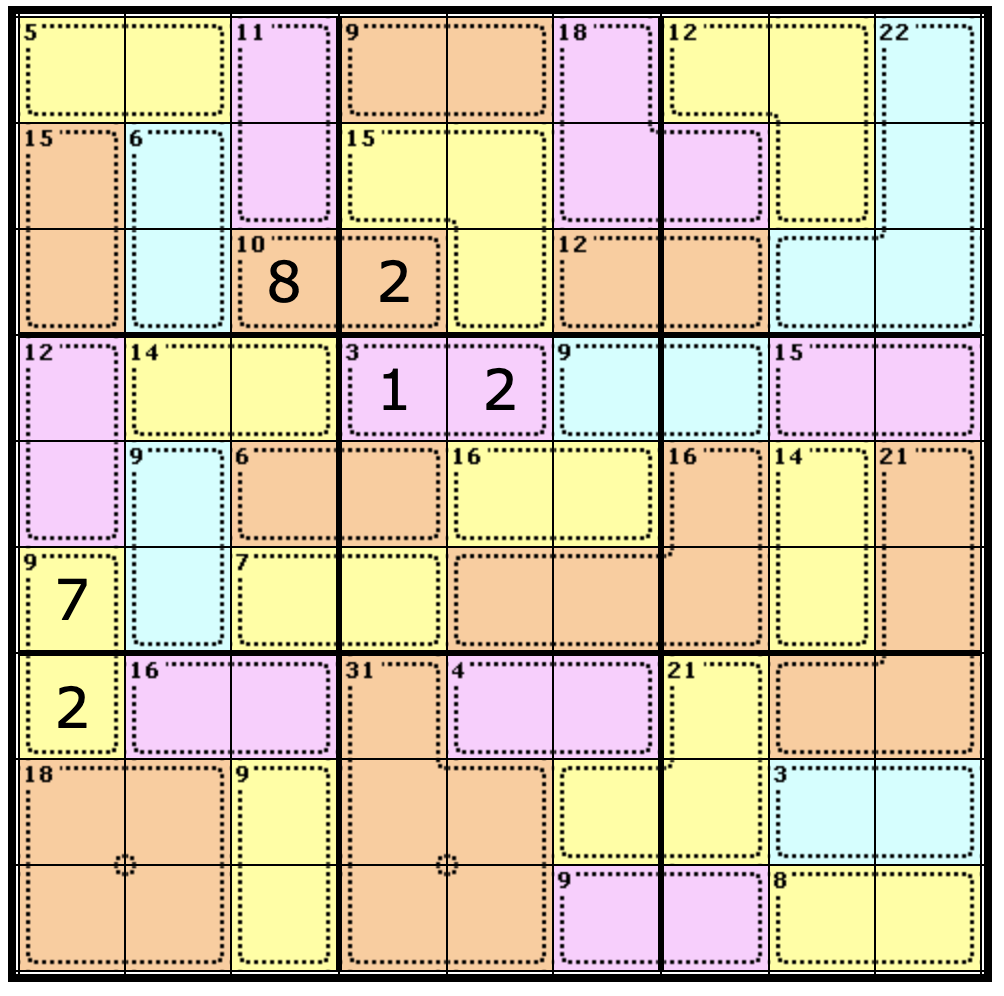
Another useful tactic for solving Killer Sudoku puzzles is to look for small Cages with very large numbers in them. That’s because they often will only have a handful of possible combinations. Take another look at the Nonet on the top left of the puzzle. 

Note the orange two square Cage with a 15 in it. The only potential number combinations to get 15 in a two square Cage are:

    • 9 and 6

    • 8 and 7

But, if you take a look at the puzzle again, you will notice that the Nonet already has an 8 in it. The Column also has a 7. This rules out the 8 and 7 combination, because of the Rule of 1 (each number can only appear once per column, row, or nonet).

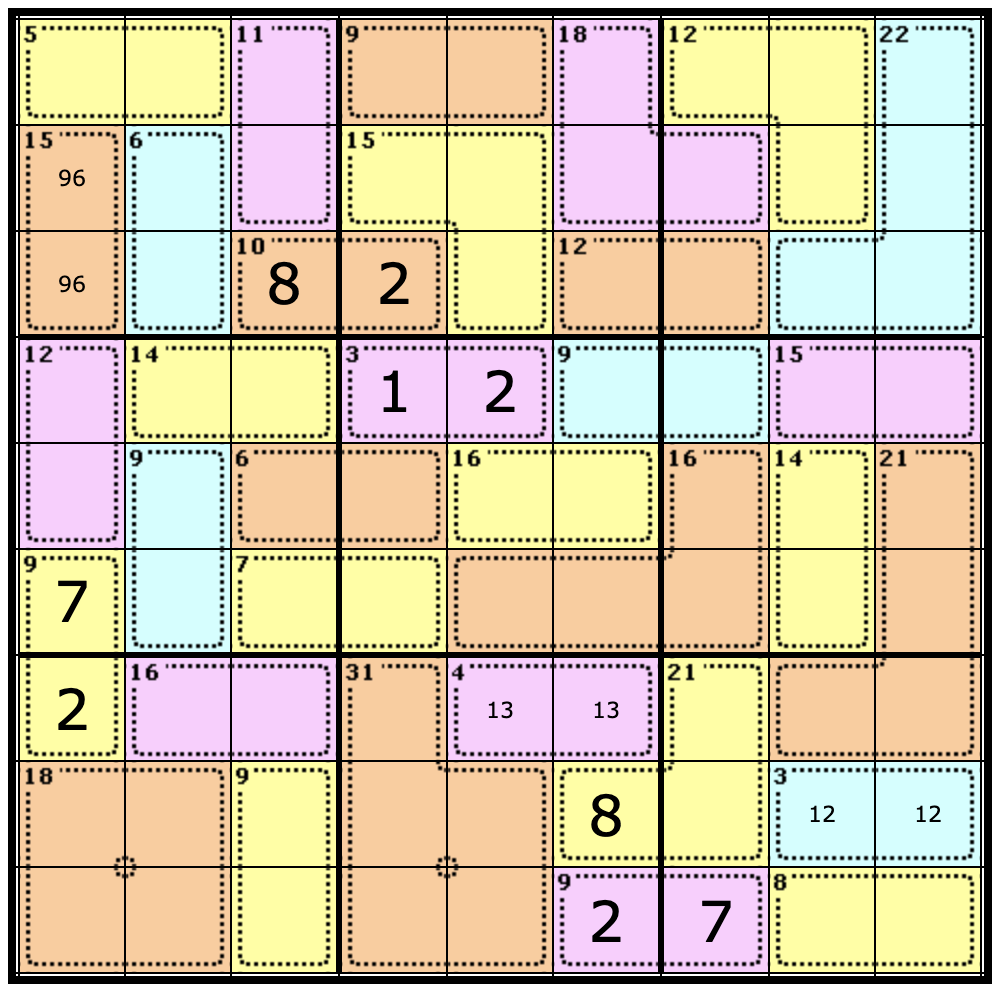
We don’t know which square has the 6 and which has the 9. As a result, we can only pencil those numbers in. This is the act of writing the numbers in small print, to remind ourselves that they cannot be used elsewhere in the column, row, or nonet, like so:

Another great place to look for solutions is areas where you used the same number several times. For example, we have used a few 2’s in our puzzle so far. If you look at the bottom middle Nonet, you will notice that 2’s can no longer go in the first or second columns or the top row, because 2’s are already present (marked in black):

That means a 2 must go in either the yellow or pink square in the middle bottom Nonet. But which one? We can look around the Nonet for clues. One clue that stands out to me is the two square blue Cage with a 3 clue to the right of the Nonet. A 2 square 3 Cage must have a 1 and a 2 in it. That eliminates 2 from that row:

That leaves us with only one location for the 2 to go. We can also fill in the 7 in that Cage, like so:

Every time you solve a square, remember to check if one of our rules can now be applied. For example, adding the 2 in the pink square of the bottom middle nonet now means we have 2 complete Cages (the 31 and the 4), along with our completed pink square and an empty yellow Cell. 

We can now apply the Rule of 45 to determine what is in the yellow square. It would be 45 - (2 + 31 + 4), which equals 8, like so (note I’ve penciled in some squares): 

You can use these basic techniques to complete the rest of the puzzle, which would look like: